责任编辑:匿名 (未验证)
2013/04/29
作者:Ashutosh Goel 赖天明(译)
一、介绍
据预测,全球的光纤器件市场到2017年将达到420亿美元的规模,要达到这种规模需要通过持续增长的对基于光纤带宽的需求来驱动,以及随之带来的强劲的移动互联网发展和更大面积的FTTx相关项目的部署来驱动。这种增长的需求对光纤在不同应用条件下部署的机械可靠性提出了严峻的挑战,因为这需要光纤在尽可能长的使用寿命内都保持最佳的工作状态,而不必在光学性能上做任何妥协。
二、光纤的使用寿命
强度分布是光纤机械可靠性模型的一个关键因素,被用来预测光纤在运行期间应力条件下所能达到的使用寿命。尽管所有研究模型类型都基于硅质光纤的裂纹传播理论,但是幂次法则理论仍然是迄今最为有效的理论,它通过对裂纹扩展建模来预测光纤工作寿命,反映出了环境依赖裂纹生长参数对光纤使用寿命的影响。
根据国际电工委员会(IEC)的IE C /TR 62048 技术报告,基于幂次法则理论的光纤在线使用寿命的计算方程式如下(1)
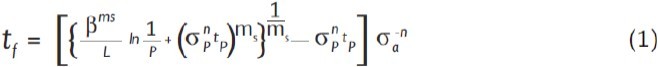
这里tf是指光纤在持续应力或静态疲劳测试条件下的使用寿命,ms是静态疲劳条件下的威布尔(Weibull)系数,β是威布尔β值, a是施加在光纤上的静态疲劳应力,
a是施加在光纤上的静态疲劳应力, p试验应力(0.72 G Pa),tp是应力施加的时间,L是被均匀施加了应力的光纤长度,或等效的张力长度,n是应力腐蚀参数,P是光纤维持工作状态的可能性。
p试验应力(0.72 G Pa),tp是应力施加的时间,L是被均匀施加了应力的光纤长度,或等效的张力长度,n是应力腐蚀参数,P是光纤维持工作状态的可能性。
这个由IEC建议的方程式IEC /TR 62048((上文方程式(1))与Griffioen et al.提出的长距离光纤张力测试方程式等效(下文方程式(2)。
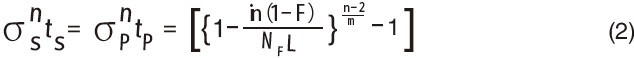
这里的 s是指在线应力,ts是光纤使用寿命,
s是指在线应力,ts是光纤使用寿命, p是试验应力,tp是试验应力施加在光纤上的时间,F是光纤失效的可能性,L是光纤长度,Np是单位长度上断裂的次数,m是外部裂纹分布得到的威布尔(Weibull)系数。
p是试验应力,tp是试验应力施加在光纤上的时间,F是光纤失效的可能性,L是光纤长度,Np是单位长度上断裂的次数,m是外部裂纹分布得到的威布尔(Weibull)系数。
依据IEC /TR 62048,斯德雷特科技有限公司使用方程式(2)来预测光纤的服务年限。关于使用该理论来预测光纤机械可靠性的详细方法介绍已经整理成文《预测光纤的机械可靠性》。该文中基于上文方程式(2)的理论得出的光纤的预期使用寿命数据,如下表:
三、总结
幂次法则理论已经被用来预测斯德雷特光纤的机械可靠性,并针对具体的应用对应力水平提出了指导。要获得最佳的可靠性,长期应力大小不应超过试验应力的五分之一(22kpsi),短期应力不因超过试验应力的三分之一(36kpsi)。
据预测,全球的光纤器件市场到2017年将达到420亿美元的规模,要达到这种规模需要通过持续增长的对基于光纤带宽的需求来驱动,以及随之带来的强劲的移动互联网发展和更大面积的FTTx相关项目的部署来驱动。这种增长的需求对光纤在不同应用条件下部署的机械可靠性提出了严峻的挑战,因为这需要光纤在尽可能长的使用寿命内都保持最佳的工作状态,而不必在光学性能上做任何妥协。
二、光纤的使用寿命
强度分布是光纤机械可靠性模型的一个关键因素,被用来预测光纤在运行期间应力条件下所能达到的使用寿命。尽管所有研究模型类型都基于硅质光纤的裂纹传播理论,但是幂次法则理论仍然是迄今最为有效的理论,它通过对裂纹扩展建模来预测光纤工作寿命,反映出了环境依赖裂纹生长参数对光纤使用寿命的影响。
根据国际电工委员会(IEC)的IE C /TR 62048 技术报告,基于幂次法则理论的光纤在线使用寿命的计算方程式如下(1)
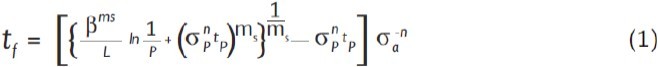
这里tf是指光纤在持续应力或静态疲劳测试条件下的使用寿命,ms是静态疲劳条件下的威布尔(Weibull)系数,β是威布尔β值,
 a是施加在光纤上的静态疲劳应力,
a是施加在光纤上的静态疲劳应力, p试验应力(0.72 G Pa),tp是应力施加的时间,L是被均匀施加了应力的光纤长度,或等效的张力长度,n是应力腐蚀参数,P是光纤维持工作状态的可能性。
p试验应力(0.72 G Pa),tp是应力施加的时间,L是被均匀施加了应力的光纤长度,或等效的张力长度,n是应力腐蚀参数,P是光纤维持工作状态的可能性。这个由IEC建议的方程式IEC /TR 62048((上文方程式(1))与Griffioen et al.提出的长距离光纤张力测试方程式等效(下文方程式(2)。
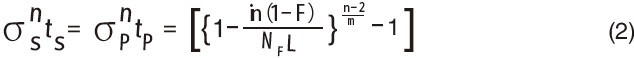
这里的
 s是指在线应力,ts是光纤使用寿命,
s是指在线应力,ts是光纤使用寿命, p是试验应力,tp是试验应力施加在光纤上的时间,F是光纤失效的可能性,L是光纤长度,Np是单位长度上断裂的次数,m是外部裂纹分布得到的威布尔(Weibull)系数。
p是试验应力,tp是试验应力施加在光纤上的时间,F是光纤失效的可能性,L是光纤长度,Np是单位长度上断裂的次数,m是外部裂纹分布得到的威布尔(Weibull)系数。依据IEC /TR 62048,斯德雷特科技有限公司使用方程式(2)来预测光纤的服务年限。关于使用该理论来预测光纤机械可靠性的详细方法介绍已经整理成文《预测光纤的机械可靠性》。该文中基于上文方程式(2)的理论得出的光纤的预期使用寿命数据,如下表:
表1 基于定长的光纤期望寿命与不同应力条件的关系¹
| 施加应力 | 预期使用寿命 |
| 22kpsi | ≥40年 |
| 27kpsi | 4个月 |
| 30kpsi | 24小时 |
| 36kpsi | 5小时 |
| 54kpsi | 3秒 |
¹光纤失效的可能性<<1ppm
三、总结
幂次法则理论已经被用来预测斯德雷特光纤的机械可靠性,并针对具体的应用对应力水平提出了指导。要获得最佳的可靠性,长期应力大小不应超过试验应力的五分之一(22kpsi),短期应力不因超过试验应力的三分之一(36kpsi)。


